Spatial modeling for correlated cancers using bivariate directed graphs
Introduction
Disease mapping, which refers to techniques for mapping and analysis of geographical variations in disease rates and the investigation of environmental risk factors underlying these patterns, has long been an important tool in cancer epidemiology (1). Disease maps are used to highlight geographic areas with high and low prevalence, incidence, or mortality rates of cancers, and the variability of such rates over a spatial domain (2). They can also be used to detect “hot-spots” or spatial clusters which may arise due to common environmental, demographic, or cultural effects shared by neighboring regions (3). Maps of crude incidence or mortality rates can be misleading when the population sizes for some of the units are small, which results in large variability in the estimated rates, and makes it difficult to distinguish chance variability from genuine differences. The correct geographic allocation of health care resources can be greatly enhanced by deployment of statistical models that allow a more accurate depiction of true disease rates and their relation to explanatory variables (covariates). Many tasks critical for successful cancer surveillance and control require new inferential methods to handle these complex and often spatially indexed data sets. Since local sample sizes within each spatial region are too low for design-based solutions to attain desired levels of statistical precision (4), much recent work in disease-mapping has been carried out within the context of Bayesian hierarchical models (5). The body of scientific literature on modern methods for geographic disease mapping is too vast to be reviewed here. Comprehensive reviews of prevalent statistical disease mapping methods and their implementation using available software can be found, among several other sources (6-9).
Statistical models for mapping a single disease have employed probability distributions such as Markov random fields or MRFs (10) that introduce dependence using the adjacency information among the different regions on a map. Two conspicuous examples are the conditional autoregression (CAR) and simultaneous autoregression (SAR) models (11-14) for further discussions on CAR and SAR models. More recently, directed acyclic graphical autoregressive (DAGAR) models that employ directed acyclic graphs (DAGs) have been developed as an alternative to CAR or SAR models (15). A specific motivation for DAGAR models is that they impart greater interpretability to the spatial autocorrelation parameter.
In this article, we will perform joint spatial mapping of two different types of cancers. Joint modeling is appropriate when different diseases have been observed over the same spatial units and when the diseases themselves are related to each other, say because they share the same set of spatially distributed risk factors or the presence of one disease in a spatial unit may encourage or inhibit the presence of the second disease in the same spatial unit. In other words, we seek models to capture the spatial association for each disease as well as the association between the diseases. There is a substantial literature on multivariate disease mapping that has demonstrated, theoretically and empirically, the benefits of jointly modeling several potentially related cancers, as opposed to modeling them independently (16-20). While it has been assertively demonstrated that independent models for cancers can lead to biased results because of unaccounted associations among the cancers, the current literature is largely based on using CAR models for spatial mapping (21-23). For example, a bivariate CAR model has been proposed for modeling two associated diseases (21). Extensions such as a generalized multivariate CAR model (GMCAR) have been developed and compared with other multivariate CAR models (24,25) revealing strong correlation of mortality rates for lung and esophageal cancer (26). Our proposed bivariate DAGAR (BDAGAR) model for modeling two diseases over the same spatial region will help epidemiologists and spatial analysts better interpret the association among the cancers.
The incidence of adenocarcinoma of lung and esophageal cancer have been found to share common risk factors including gastroesophageal reflux disease (GERD), obesity and its associated metabolic syndrome (diabetes, hypertension and hyperlipidemia) (27). In terms of metabolic mechanisms, it has also been reported that cytochrome P450 2C19 (CYP2C19) may participate in the activation of procarcinogen of both lung and esophageal cancer, and CYP2C19 poor metabolizers (PMs) have higher incidence of two cancers (28). Given the potential association between the incidence of lung and esophageal cancer, the remainder of this article proceeds by developing a class of BDAGAR models, conducting some disease mapping for these two different cancers, and summarizing with some concluding remarks.
Methods
Our approach will be to construct a probability model for each disease using the distribution specified by DAGAR. We will extend the univariate DAGAR to a bivariate model by modeling the distribution of one disease as a univariate DAGAR and the conditional distribution of the second disease given the first also as a DAGAR. In this sense, our BDAGAR is analogous to the bivariate CAR models (26). We develop notations and briefly discuss the univariate DAGAR in the following section.
DAGAR for modeling a single disease
We consider a geographic map of our region of interest (e.g., a particular state) delineated by k distinct administrative regions (e.g., counties or ZIP codes) with clear non-overlapping boundaries separating them. Let w = (w1, w2, ..., wk)T be a k×1 vector consisting of spatially associated random effects corresponding to each region. We develop a spatially correlated model using a DAG. The geographic map provides us with a list of neighbors for each region. Neighbors can be defined by the user. Common definitions include when two regions share a common boundary or if their centers are within a certain fixed distance, although the model and resulting distribution theory hold for any fixed set of neighbors. The data structure for the geographic map and its neighbors is defined as a graph, denoted G = {V, E}, where the regions are indexed by an ordered set V = {1, 2, ..., k} and form the vertices of the graph and E is the collection of edges between the vertices, i.e., the collection of ordered pairs (j, j') such that j and j' are geographic neighbors based upon some specified definition.
The DAGAR model specifies w ~ N (0, τQ(ρ)), where Q(ρ) is a spatial precision matrix that depends only upon a spatial autocorrelation parameter ρ and τ is a positive scale parameter. To describe Q(ρ), we define neighbor sets N(i) = {j < i: j ~ i}, where i ∈ V\{1}, i.e., the set V excluding the region indexed by 1, and j ∈ V. Thus, N(i) includes geographic neighbors of region j that precede i in the ordered set V. The precision matrix Q(ρ) = (I − B)TF(I − B), where B is a k × k strictly lower-triangular matrix with entries bij and F is a k × k diagonal matrix with diagonal elements fii such that
where n<i is the number of members in N(i). The above definition of bij is consistent with the lower-triangular structure of B because for any j ≥ i. The derivation of B and F as functions of a spatial correlation parameter ρ is based upon forming local autoregressive models on embedded spanning trees of subgraphs of G (15).
A BDAGAR model
We now extend the DAGAR to the bivariate case, where we jointly model two cancers across regions. Let wi = (wi1, wi2, ..., wik)T be the spatial random effect vector for disease i, where wij refers to the spatial random effect for disease i in region j. We will build a hierarchical model:
where N(× | µ, Q) denotes a normal density with mean µ and precision matrix Q. The precision matrices τiQi(ρi) for i =1, 2 are the DAGAR precision matrices formed with the entries of B and F described in Eq. [1] with ρi. Therefore, in Eq. [2] we model w1 as a univariate DAGAR and w2 conditional on w1 also as a DAGAR. Each disease has its own distribution and there are two spatial autocorrelation parameters (ρ1 and ρ2) corresponding to the two diseases. This ensures that spatial associations specific to each disease will be captured.
The matrix A21 models the association between the two diseases. We use a parametric form A21 = η0Ik + η1M, where M is the binary adjacency matrix of the geographic map, i.e., mij =1 if i ~ j and 0 otherwise. The joint distribution of is now derived from Eq. [2] as w ~ N(0, Qw), where the precision matrix Qw is
and the covariance matrix is
We call a normal distribution with the above precision, or covariance, matrix, the BDAGAR model. The interpretation of ρ1 and ρ2 is clear: ρ1 measures the spatial association for the first cancer, while ρ2 is the residual spatial correlation in the second cancer after accounting for the first cancer. Similarly, τ1 is the spatial precision parameter for the first cancer, while τ2 is the residual precision for the second cancer after accounting for the first.
Model implementation
Let yij be our outcome of interest corresponding to cancer i in region j. We will assume that yij is a continuous variable, e.g., incidence rates, that is related to a set of explanatory variables through the regression model:
where xij is a pi ×1 vector of explanatory variables specific to cancer i within region j, βi is the slopes corresponding to cancer i, wij is the spatial effects that collectively follow the BDAGAR distribution described in section “A BDAGAR model”, capture additional heterogeneity and variability independent of spatial variation, where is the residual variance for cancer i. The regression model is extended to the following specific Bayesian hierarchical framework with the posterior distribution p(β, w, η, ρ, τ, σ | y) proportional to
where β = {β1, β2}, τ = {τ1, τ2}, σ = {σ1, σ2} and η = {η0, η1}, and IG(× | a, b) is the inverse-gamma distribution with shape and rate parameters a and b, respectively.
We sample the parameters from the posterior distribution in Eq. [6] using Markov chain Monte Carlo (MCMC) with Gibbs sampling and random walk metropolis (29) as implemented in the rjags package within the R statistical computing environment. To compare and assess models, we use the Widely Applicable Information Criterion (WAIC) (30,31), which is computed as
where is the expected log point-wise predictive density for a new dataset and is the estimated effective number of parameters, which is sum of posterior variance of the log predictive density for each data point. WAIC is easy to compute using posterior samples.
Results
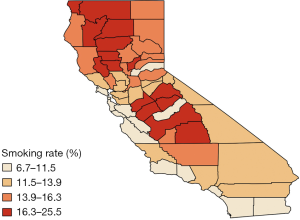
We analyze a data set extracted from the SEER*Stat database using the SEER*Stat statistical software (32). We consider 2 cancers, lung (ICD-O-3: C340-C349) and esophagus (ICD-O-3: C150-C159), where the outcome is the 5-year average crude incidence rates per 100,000 population in the years from 2012 to 2016 across 58 counties in California, USA, calculated from the software directly. County-level explanatory variables for each cancer, that possibly affect the incidence rates, are available and include adult cigarette smoking rates in percentage (smokeij), percentages of residents younger than 18 years old (youngij), older than 65 years old (oldij), with education level below high school (eduij), percentages of unemployed residents (unempij), black residents (blackij), male residents (maleij), uninsured residents (uninsureij) and percentages of families below the poverty threshold (povertyij). All covariates, except adult cigarette smoking rates, are county attributes extracted from the SEER*Stat database (33) for the years 2012–2016. As a potential common risk factor for both lung and esophageal cancer, adult cigarette smoking rates for 2014–2016 were obtained from the California Tobacco Control Program (34).
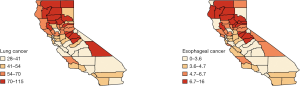
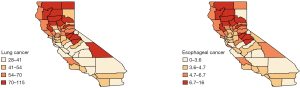
We analyzed this data set using the Bayesian hierarchical model [6]. The county-level maps of the raw incidence rates per 100,000 population for the two cancers are shown in Figure 1. The maps exhibit the evidence of correlation across space and between cancers. Cutoffs for the different levels of incidence rates are quantiles for each cancer. For both lung and esophageal cancer, in general, incidence rates are higher in counties located in the northern areas than those in southern part. The four counties in the center including Amador, Calaveras, Tuolumne and Mariposa have relatively high incidence rates compared to the neighboring counties. Overall, counties with similar levels of incidence rates tend to depict some spatial clustering.
For our analysis, we specified the following prior distribution
where Unif (× | a, b) denotes the Uniform density over (0, 1) and Qw(τ, ρ) is the BDAGAR precision matrix of w given in Eq. [3].
We fit the BDAGAR model using the two different cancer orders, i.e., [esophagus] × [lung | esophagus] and the reverse ordering [lung] × [esophagus | lung]. We will refer to these orderings simply as [lung | esophagus] and [esophagus | lung], respectively. Table 1 presents measures for model fit using the WAIC. We also compare BDAGAR with the “Generalized Multivariate Conditional Autoregression (GMCAR)” models (26). In both BDAGAR and GMCAR models, the conditional order [esophagus] × [lung | esophagus] has a smaller WAIC (hence better fit to the data) than the reverse ordering. Meanwhile, within each order, BDAGAR seems to excel over the GMCAR with lower scores in both model fit and effective number of parameters, as seen in the values of and , respectively. The preference of WAIC for [lung | esophagus] is also corroborated by the posterior distribution of η0 and η1 from BDAGAR shown in Figure 2. In [esophagus | lung], the parameter η1 has posterior mean of −1.94 and a 95% credible interval (−3.94, −0.58). This shows significant negative values that offset part of the significant positive effect of η0 with a mean of 7.58 and a 95% credible interval of (2.82, 13.94). For [lung | esophagus], η0 is significantly positive with a mean of 17.58 and 95% credible interval of (11.62, 27.84), while η1 tends to be positive with a mean of 1.1 but with a 95% credible interval (−0.77, 2.73) that includes 0. Consequently, we present the following results and analysis for [lung | esophagus] which seems to be the preferred model.
Table 1
| Model | lppd | pWAIC | WAIC |
|---|---|---|---|
| BDAGAR (esophagus | lung) | −261.31 | 45.32 | 613.27 |
| BDAGAR (lung | esophagus) | −155.12 | 51.72 | 413.68 |
| GMCAR (esophagus | lung) | −264.51 | 46.09 | 621.19 |
| GMCAR (lung | esophagus) | −156.51 | 52.05 | 417.12 |
BDAGAR, bivariate directed acyclic graphical autoregressive; GMCAR, generalized multivariate conditional autoregression; WAIC, Widely Applicable Information Criterion.
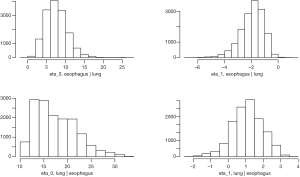
Table 2 summarizes the parameter estimates from the BDAGAR model corresponding to [lung | esophagus]. For fixed effects, the increasing percentage of residents younger than 18 years old significantly reduces the incidence rate for esophageal cancer, while the percentage of residents older than 65 years old has a significantly opposite effect for lung cancer. Unsurprisingly, higher adult cigarette smoking rates significantly increase the incidence rates for both lung and esophageal cancer. After accounting for these explanatory variables, the residual random effects still exhibit spatial association patterns for both cancers. Turning to spatial correlations, ρ1 measures the residual spatial correlation (posterior mean 0.08) for esophageal cancer after accounting for the explanatory variables and ρ2 measures the spatial correlation (posterior mean 0.5) for lung cancer after accounting for the explanatory variables and also the effect of esophageal cancer. The small point estimates and narrower credible interval for ρ1 indicate greater confidence in weaker spatial correlation for esophageal cancer; the moderate value of ρ2 and a wider credible interval suggest higher spatial correlation for lung cancer. Turning to the spatial precision of random effects for each cancer, the estimates of {τ1, τ2} are indicative of esophageal cancer having larger variability, although we must keep in mind that τ2 is the conditional marginal precision for lung cancer after accounting for esophageal cancer and, therefore, may not be directly comparable to τ1.
Table 2
| Parameters | Esophagus | Lung |
|---|---|---|
| Intercept | 18.75 (4.55, 32.72) | 7.19 (−47.07, 61.87) |
| Smoke | 0.27 (0.12, 0.41) | 1.27 (0.28, 2.3) |
| Young | −0.23 (−0.45, −0.01) | −0.75 (−1.94, 0.44) |
| Old | 0.14 (−0.03, 0.31) | 2.61 (1.62, 3.61) |
| Edu | 0.02 (−0.1, 0.14) | −0.25 (−1.04, 0.54) |
| Unemp | −0.07 (−0.26, 0.12) | 0.52 (−0.79, 1.84) |
| Black | 0.16 (−0.08, 0.39) | 0.8 (−0.82, 2.41) |
| Male | −0.04 (−0.19, 0.12) | 0.14 (−0.95, 1.26) |
| Uninsure | −0.31 (−0.53, −0.09) | −0.08 (−1.11, 0.94) |
| Poverty | 0.32 (−0.33, 0.96) | 0.23 (−3.96, 4.48) |
| ρi | 0.08 (0, 0.25) | 0.5 (0.03, 0.97) |
| τi | 2.72 (0.96, 6.69) | 19.41 (2.47, 54.36) |
| 2.05 (1.39, 3.05) | 0.93 (0.18, 3.87) |
BDAGAR, bivariate directed acyclic graphical autoregressive.
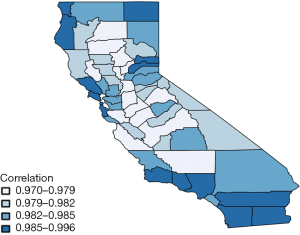
Figure 3 shows the estimated correlation between lung and esophageal cancer in each of 58 counties. This map also seems to be consistent with the estimates of η. Correlations between lung and esophageal cancers in all counties are significantly positive with large means at around 0.97−1 which are due to the highly positive values in η0. This indicates that esophageal cancer is highly correlated with lung cancer. However, in general, the correlation between the two cancers increases slightly from the center to marginal areas, especially for those with fewer counties in the neighborhood.
Finally, Figure 4 provides further visual corroboration of the goodness of fit for the BDAGAR mode corresponding to [lung | esophagus]. Here, we see that the posterior mean of the incidence rates for lung and esophageal cancer are very consistent with the raw incidence rates shown in Figure 1. Given the significant effect of adult cigarette smoking rates on incidence rates for both cancers, the higher fitted incidence rates in the northern areas are in accordance with higher smoking rates in same counties as shown in Figure 5. Though the smoking rates are also high in the middle part, the relatively lower fitted incidence rates may be due to the offset of negative spatial random effects for these counties.
Discussion
We have extended a recently proposed class of DAGAR models (15) for univariate disease mapping to bivariate “BDAGAR” models that can be applied to estimate spatial correlations for two correlated cancers. The BDAGAR model retains the interpretation of DAGAR models clearly separating the spatial correlation for each cancer from any inherent or endemic association between the two cancers. The BDAGAR model can still be efficiently computed using MCMC algorithms. Our analysis of incidence rates from lung and esophagus cancer demonstrates the efficiency of BDAGAR and its improved performance, as measured by WAIC, over existing alternatives such as the GMCAR models. In fact, it has been reported that DAGAR tended to outperform CAR in univariate models (15). It is, therefore, not unexpected that BDAGAR will outperform the bivariate CAR models. We are currently exploring these issues in greater detail and even extending our analysis to more than two cancers. We expect to report our findings in future manuscripts.
While we have restricted our attention only to cancer incidence rates, BDAGAR models can also be used with time-to-event data to investigate geographical patterns in the hazard function. For example, each patient in a study may provide multiple survival times from the onset of each of two cancers along with his or her county of residence. The BDAGAR model can become an excellent alternative to CAR and different MCAR models in spatial survival analysis (18,25,35-37).
The BDAGAR models developed here proceeds from conditional specifications. Concerns may arise over the ordering of the variables in the hierarchical approach. While in the case of a few cancers, such as 2 in our case, one can evaluate models arising from the different orders, this strategy will become cumbersome with several cancers. For instance, even with 4 cancers, we will have 24 different models that will need to be evaluated and compared. This becomes impractical. A joint modeling approach, analogous to order-free MCAR models (22), can build rich spatial structures from linear transformations of simpler latent variables. For instance, we can develop alternate multivariate DAGAR, or MDAGAR models, using w = Λf, where Λ is a suitably specified square matrix and f is a latent vector whose components follow independent univariate DAGAR distributions. Note that by modeling the joint distribution, the incompatibility of conditional model building (i.e., different joint distributions for different orderings) is avoided. However, the issue of the identifiability of Λ is raised, and careful specification of its structure is needed. These approaches will be further investigated elsewhere.
Finally, we caution against using the BDAGAR models developed here for causal inference because of the potential limitations of DAGs in causal analysis. While DAGs assume that relationships are directed and acyclic, truly cyclical or bidirectional relationships may exist as exceptions in causal processes (38). Moreover, the discrete observations DAGs hardly fully capture the underlying time-continuous causal processes and as a result, the conditional independence in DAGs can rarely be identified with causal structure (39). Instead, these models should be used for evincing relationships between the cancers and the strengths of spatial association for each cancer to posit new hypotheses and generate further research. For example, one such finding from these models is that the spatial association exhibited by esophageal cancer seems to be considerably less pronounced than for lung cancer (after controlling for esophageal cancer). This finding is similar to those from earlier spatial analysis of mortality rates for these two cancers (21). Whether this is an artefact of the model itself or of the specific dataset analyzed here or a result of further explanatory variables not accounted for here will need to be further investigated elsewhere.
Acknowledgments
Funding: The work of the first and second authors have been supported in part by the Division of Mathematical Sciences (DMS) of the National Science Foundation (NSF) under grant 1916349 and by the National Institute of Environmental Health Sciences (NIEHS) under grants R01ES030210 and 5R01ES027027. The work of the third author was supported by the Division of Mathematical Sciences (DMS) of the National Science Foundation (NSF) under grant 1915803.
Footnote
Provenance and Peer Review: This article was commissioned by the Guest Editors (Peter Baade and Susanna Cramb) for the series “Spatial Patterns in Cancer Epidemiology” published in Annals of Cancer Epidemiology. The article has undergone external peer review.
Data Sharing Statement: Available at https://ace.amegroups.com/article/view/10.21037/ace-19-41/dss
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://ace.amegroups.com/article/view/10.21037/ace-19-41/coif). The series “Spatial Patterns in Cancer Epidemiology” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Koch T. Cartographies of disease: maps, mapping, and medicine. Redlands, CA: Esri Press, 2005.
- Waller LA, Carlin BP, Xia H, et al. Hierarchical spatio-temporal mapping of disease rates. J Am Stat Assoc 1997;92:607-17. [Crossref]
- Banerjee S. Spatial Data Analysis. Annu Rev Public Health 2016;37:47-60. [Crossref] [PubMed]
- Schaible WL. Indirect estimators in US federal programs. vol. 108. Springer Science & Business Media, 2013.
- Banerjee S, Carlin BP, Gelfand AE. Hierarchical modeling and analysis for spatial data. Boca Raton, FL: CRC Press, 2014.
- Best N, Richardson S, Thomson A. A comparison of Bayesian spatial models for disease mapping. Stat Methods Med Res 2005;14:35-59. [Crossref] [PubMed]
- Waller L, Carlin B. Handbook of Spatial Statistics. Gelfand AE, Diggle PJ, Fuentes M, et al. editors. Boca Raton, FL: Taylor and Franci. USA: Chapman and Hall CRC Press, 2010.
- Waller LA, Gotway CA. Applied spatial statistics for public health data. vol. 368. John Wiley & Sons, 2004.
- Lawson AB. Statistical methods in spatial epidemiology. John Wiley & Sons, 2013.
- Rua H, Held L. Gaussian Markov Random Fields: Theory and Applications. Monographs on statistics and applied probability. Boca Raton, FL: Chapman and Hall/CRC Press, 2005.
- Besag J. Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society: Series B (Methodological) 1974;36:192-236. [Crossref]
- Besag J, York J, Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann Inst Stat Math 1991;43:1-20. [Crossref]
- Anselin L. Lagrange Multiplier Test Diagnostics for Spatial Dependence and Spatial Heterogeneity. Geographical Analysis 1988;20:1-17. [Crossref]
- Kissling WD, Carl G. Spatial autocorrelation and the selection of simultaneous autoregressive models. Global Ecology and Biogeography 2008;17:59-71.
- Datta A, Banerjee S, Hodges JS, et al. Spatial disease mapping using directed acyclic graph auto-regressive (DAGAR) models. Bayesian Analysis 2019;14:1221-44. [Crossref]
- Knorr-Held L, Best NG. A shared component model for detecting joint and selective clustering of two diseases. Journal of the Royal Statistical Society: Series A (Statistics in Society) 2001;164:73-85. [Crossref]
- Held L, Natário I, Fenton SE, et al. Towards joint disease mapping. Stat Methods Med Res 2005;14:61-82. [Crossref] [PubMed]
- Diva U, Dey DK, Banerjee S. Parametric models for spatially correlated survival data for individuals with multiple cancers. Stat Med 2008;27:2127-44. [Crossref] [PubMed]
- Martinez-Beneito MA. A general modelling framework for multivariate disease mapping. Biometrika 2013;100:539-53. [Crossref]
- Marí-Dell’Olmo M, Martinez-Beneito MA, Gotsens M, et al. A smoothed ANOVA model for multivariate ecological regression. Stoch Environ Res Risk Assess 2014;28:695-706. [Crossref]
- Kim H, Sun D, Tsutakawa RK. A Bivariate Bayes Method for Improving the Estimates of Mortality Rates With a Twofold Conditional Autoregressive Model. J Am Stat Assoc 2001;96:1506-21. [Crossref]
- Jin X, Banerjee S, Carlin BP. Order-free co-regionalized areal data models with application to multiple-disease mapping. J R Stat Soc Series B Stat Methodol 2007;69:817-38. [Crossref] [PubMed]
- Zhang Y, Hodges JS, Banerjee S. Smoothed ANOVA with spatial effects as a competitor to MCAR in multivariate spatial smoothing. Ann Appl Stat 2009;3:1805-30. [Crossref] [PubMed]
- Gelfand AE, Vounatsou P. Proper multivariate conditional autoregressive models for spatial data analysis. Biostatistics 2003;4:11-25. [Crossref] [PubMed]
- Carlin BP, Banerjee S. Hierarchical multivariate CAR models for spatio-temporally correlated survival data. Bayesian Statistics 2003;7:45-63.
- Jin X, Carlin BP, Banerjee S. Generalized hierarchical multivariate CAR models for areal data. Biometrics 2005;61:950-61. [Crossref] [PubMed]
- Agrawal K, Markert RJ, Agrawal S. Risk factors for adenocarcinoma and squamous cell carcinoma of the esophagus and lung. AME Med J 2018;3:35. [Crossref]
- Shi WX, Chen SQ. Frequencies of poor metabolizers of cytochrome P450 2C19 in esophagus cancer, stomach cancer, lung cancer and bladder cancer in Chinese population. World J Gastroenterol 2004;10:1961-3. [Crossref] [PubMed]
- Gamerman D, Lopes HF. Markov chain Monte Carlo: stochastic simulation for Bayesian inference. Chapman and Hall/CRC, 2006.
- Watanabe S. Asymptotic equivalence of Bayes cross validation and widely applicable in- formation criterion in singular learning theory. Journal of Machine Learning Research 2010;11:3571-94.
- Gelman A, Hwang J, Vehtari A. Understanding predictive information criteria for Bayesian models. Statistics and Computing 2014;24:997-1016. [Crossref]
- Step 1: Calculating Age-adjusted Rates - SEER*Stat Tutorials. Available online: https://seer.cancer.gov/seerstat/tutorials/aarates/step1.html
-
Static County Attributes – SEER Datasets - California Department of Public Health, California Tobacco Control Program. California Tobacco Facts and Figures 2018. Sacramento, CA: California Department of Public Health, 2018.
- Banerjee S, Wall MM, Carlin BP. Frailty modeling for spatially correlated survival data, with application to infant mortality in Minnesota. Biostatistics 2003;4:123-42. [Crossref] [PubMed]
- Banerjee S, Dey DK. Semiparametric proportional odds models for spatially correlated survival data. Lifetime Data Anal 2005;11:175-91. [Crossref] [PubMed]
- Cooner F, Banerjee S, McBean AM. Modelling geographically referenced survival data with a cure fraction. Stat Methods Med Res 2006;15:307-24. [Crossref] [PubMed]
- Pearce N, Lawlor DA. Causal inference-so much more than statistics. Int J Epidemiol 2016;45:1895-903. [Crossref] [PubMed]
- Aalen OO, Røysland K, Gran JM, et al. Can we believe the DAGs? A comment on the relationship between causal DAGs and mechanisms. Stat Methods Med Res 2016;25:2294-314. [Crossref] [PubMed]
Cite this article as: Gao L, Banerjee S, Datta A. Spatial modeling for correlated cancers using bivariate directed graphs. Ann Cancer Epidemiol 2020;4:8.